Soil Engineering

Keywords: planimeter, Computation of area, zero circle
Instrumental methods are one of the important technique uses to determine area of a plot. The other methods for area computation are using field notes and from previously plotted plan. We have already discussed them here.
Computation of areas and volumes | Computation of Area from Plan

Significance of Planimeter in Area computation
The planimeter gives more accurate (within one percent) results compared to the other methods except by direct calculation from the field notes. It is used for determining the areas of figures plotted to scale, especially when the boundaries are irregular. Example for such plots are, plot with irregular boundary and plot having a river as boundary on one side.
Read More

Keywords: graphical methods, area computation, mid ordinate rule, trapezoid rule, Simpson’s rule, Parabolic rule

This article discusses the second method for computation of area (i.e., from previously plotted plan). You can read the first method ( computation of area using field notes) here.

Several methods can be used to determine the areas from plans. These methods are generally classified as graphical methods and instrumental methods

1) Graphical methods
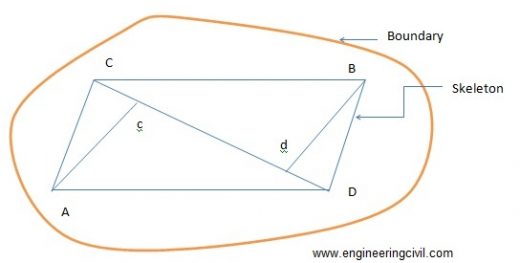
These methods use the measured data from the existing plan. The areas may be calculated for the area as a whole or the areas is found by adding the areas of the skeleton and the area of the irregular strip between the skeleton and the boundary.

a) Entire areas
Generally used methods to calculate the area as whole is enumerated as follows:

i) By division of the area into triangles
In this method the total area is divided into a number of triangles. The base and altitude of each triangle are, measured and its area is found. When the boundaries are irregular, straight lines termed as ‘give and take’ or ‘equalizing lines’ replace them. These lines are so drawn that they exclude as much as they include as shown in figure.

ii) By division of the area into squares
This method is explains by figure. A piece of tracing paper is divided into squares of equal areas. This is place over the drawing. The total number of complete squares and fractions of squares formed along the boundaries are estimated in terms of full squares. The area of the plan is equal to the number of square’s multiplies by the area of one square.

iii) By division of the area into trapezoids
A number of equidistant parallel lines are drawn on a tracing paper and the tracing paper is placed over the plan so that the area is exactly enclosed between two parallel lines. Then the plotted area is divided into a number of strips. The curved ends of which are replaced by perpendicular ‘give and take’ lines. The sum of the base length of the rectangles thus obtains, multiplied by the common distance between the parallel lines gives the area of the plan.

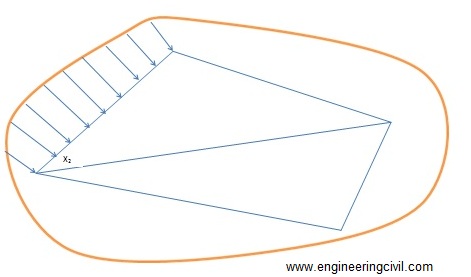
b) Areas along boundaries
The areas enclosed between the adjacent survey lines and the curved boundaries are determined by using ordinated. The survey line is divided into a number of equal parts and the ordinate at each point is drawn and scaled. The area can be calculated by several methods as described below:

i) Mid ordinate rule
Ordinates are measured at the midpoint of each division.

Area= (h₁+h₂+h₃+……+h_n) L/n

Area= (h₁+h₂+h₃+…..+h_n) d

Where
h₁,h₂,h₃,h₄…..,h_n= ordinates at the midpoint of each division
L= length of the base line
n= the number of equal parts into which the baselines is divided
d= the common distance between the ordinates=L/n

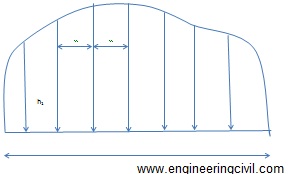
Figure 1: Illustration of mid ordinate rule

ii) Trapezoid rule
This rule is more accurate than the mid-ordinate and the average ordinate rules. To apply this method, the whole area has to be divided into a number of trapezoids. The rule can be stated as ‘to the sum of the first and last ordinates, ass twice the sum of the intermediate ordinates. Then multiply the total sum with the common distance between the ordinates. The one half of this product gives the required area’

Area=d/2 {O₀+O_n+2(O₁+O₂+….+O_n)}

When the baseline cuts the boundary at one or both ends, then O₀ or O_n are zero. In that case O₀ and O_n becomes zero in the equation above.

The trapezoid rule assumes that the boundaries between the ends of the ordinates are straight lines. The derivation of the formula is simple and can be tried out.

iii) Simpson’s rule or Parabolic rule
The rule may be stated as ‘to the sum of the first and last ordinates, add twice the sum of the remaining odd ordinates and four times the sum of all the even ordinates. Multiply the total sum thus obtained by one-third f the common distance between the ordinates. This gives the area requires’

Area-d/3 {O₀+O_n+2 (O₂+O₄+O₆+….) 4 (O₁+O₃+O₅…)}

This method requires that there be an even number of divisions of the area. If there is odd number of divisions, the area of the last division must be calculated separately and added to the result obtained by applying the Simpson’s rule to the remaining even divisions.It is to be noted that an odd number of ordinates corresponds to an even number of divisions.

The second method to calculate area from a previously plotted plan (i.e. instrumental methods) is discussed here.

Keywords: computation of area, computation volume, area calculation of irregular boundaries

This article discusses the methods which are used to determine the areas of lands and the volumes of earthwork (either cutting or filling). These methods find application in determining the areas of existing plots. Volume determination is useful to determine the volumes of cutting through elevated areas and volume of embankment for the purpose of laying routes through low lying areas.

Computation of areas
Area of land means the area as projected on a horizontal plane. The important point is,it is not the actual area of surface.
1) To determine the area of a plot with straight boundaries, the plot is then subdivided into areas having straight boundaries (i.e. triangles, rectangles or trapezium) and the area calculated using appropriated formulas for this subdivided plots.

2) To determine areas with irregular boundaries, the plot is then subdivided into areas (of regular polygons) leaving the strip of irregular land along the boundaries whose area is determined separately and added to the calculated of regular polygons.

Area is determined by two methods namely:
1. By direct use of field notes
2. From previously plotted plan

The first method for the computation of areas, i.e., the area determination using field notes is explained as follows:

Area determined by directly using the field notes
To determine the area using this method, it is not necessary to draw the whole plan to scale. Because the accuracy of the work is solely depend on the accuracy of the fieldwork, which is already done. In doing the fieldwork, as much of the whole area as possible is to be included for accuracy. The survey lines shouldlie down carefully for this.This is shown in figure 1 as follows:

Figure 1: Planning of the survey lines for the determination of area

The calculation of the plot area consists of two parts namely:
i.Calculation of the areas of the skeletons
ii.Calculations of the area enclosed between the surveys lines of the skeleton and the irregular boundaries.

Determination of the areas of the skeletons
a. By geometry
The areas of the triangles forming skeletons may be calculated by the following formulae:
1) Area of triangle= ?[s(s-a)(s-b)(s-c)]
Where a, b and c denotes the sides of the triangle
Semi-perimeter, s = (a+b+c)/2

2) Area of triangle=bh/2
Where b is the length of any side and h is the perpendicular distance from this side.

b) Area by co-ordinates
This method is used in the case of traverse survey. In this method of survey, first, a set of points well distributed in the area to be measured is selected. These points are joined by survey lines from which perpendicular offsets may be taken to the boundary. The measurements to be taken in such a traverse survey are essentially the distance of the lines connecting the points and the angle between successive lines or the bearings of the lines (bearing is the angle between the north direction and the line, measures clockwise from north).

The step wise procedures are given below:

• Arrange the co-ordinates in an order.
• Find the sum of the product of the co-ordinates joined by full lines, and the sum of the products of the co-ordinates joined by broken lines.
• Find the difference between the sums
• This difference is equal to twice the area of the traverse.
• Half this difference =area of the traverse

Determination of the area enclosed between the surveys lines of the skeleton and the irregular boundaries
To determine the areas of strips of land along the foundation, the adjoining survey line is decided into intervals and the offset to the boundary is measured at each point. The areas of the irregular strips may now be calculated by multiplying the mean of each successive pair of adjacent offsets by the distance between them as shown in figure 2.

O₁= offset at chainage X₁

O₂= Offset at chainage X₂

Mean offset= (O₁+O₂)/2

Distance between the offsets = X_2-X₁

Area of the portion between the skeleton X₂ and X₁ and the boundary = {(O₁+O₂)/2}(X_2-X₁)

Figure 2: Determination of the area along boundaries

The second method for the computation of area (i.e. computation of area from previously plotted plan) is discussed here.

Geotechnical Investigation of a Construction Site
A civil engineer needs to understand the soil behavior of the construction site and to find the satisfactory solution to the soil problem. The knowledge of subsoil conditions at a site is a prerequisite for safe and economical design of sub-structural elements. A well planned and properly executed site investigation programme will provide information about the stratigraphy and physical properties of the soil at the site including ground water table and its fluctuations. The process of investigation are as follows:

Sub-surface Investigation:
Preliminary Exploration which is study of geology of the site and the reconnaissance.Detailed investigation follows the preliminary investigation and from this we come to know about the nature, sequence and thickness of soil layers and lateral variations, sequence and position of ground water table.

Borehole:
As a part of geotechnical investigation,we need to construct boreholes.There are different methods used for boring.e.g. Auger Boring,Wash Boring,Percussion Boring, Rotary Boring etc. The suitability of any particular method of boring depends mainly on the nature of soil,the position of water table,the ease and accuracy with which changes in soil and ground water conditions can be determined.

Soil Sample:
Generally it can be classified as
(i) Disturbed Sample: Disturbed Sample are those where natural soil structure gets modified or disturbed during sampling procedure.
(ii) Undisturbed sample: Here original soil structure is preserved and also soil properties have not undergone any alteration or modification.

For all practical purpose, undisturbed soil sample is suitable for all laboratory tests including shear strength and consolidation tests.

Types of soil samples Required for Laboratory Tests

Type of Test	Type of sample required
Natural water content	Undisturbed
Density	Undisturbed /Representative
Specific Gravity	Undisturbed / Representative
Grain size distribution	Undisturbed
Atterberg’s Limit	Undisturbed
Coefficient of permeability	Undisturbed
Consolidation parameters	Undisturbed
Shear strength parameters	Undisturbed

Field Tests:
The field tests commonly used in sub-surface investigation are:

(i) Vane Shear Test
(ii) Plate Load Tests
(iii) Standard Penetration Test(SPT)
(iv) Cone Penetration Test
(v) Pressure Meter Test
(vi) Geophysical Methods

Number and Deposition of Trial Pits and Borings
The purpose of soil exploration is to provide the designer with complete information about the subsoil layers at the site. The number and spacing of boreholes or trial pits depend upon extent of site, uniformity of strata, nature of structure and loading diagram.

As per IS:1892-1979 recommendations,for a compact building site covering an area of about 0.4 hectare,one bore hole or trial pit in the center and one at each corner will be sufficient.For larger areas,it may be useful to perform sounding test /cone penetration tests at a spacing of 50m to 100 m by dividing the area in a grid pattern.

Borehole Logs:
After the soil investigation has been completed and the results of laboratory tests become available, the ground conditions discovered in each boreholes are summarized in the form of a chart called borehole log. A borehole log contains following data-

(i) The soil profile with elevations of different strata
(ii) Ground water table
(iii) Termination level of borehole
(iv) The depth or range of depth at which samples are taken
(v) Depths at which in-situ tests were performed
(vi) Type of soil sample
(vii) Results of important laboratory tests
(viii) N-values at the measured elevations

A sample of borehole log is shown below

Fig 1 : BORE HOLE CHART

Site Investigation Report:
A site investigation report is the conclusion of the investigation, exploration and testing programme. The report is addressed to the client. Although individual reports may be given in the form of content and presentation, a typical report contains:

(i) Introduction
(ii) Borehole logs
(iii) Field and laboratory tests results
(iv) Analysis of data
(v) Recommendation
(vi) Reference

Soil classification is the arrangement of soils into different groups such that the soils in a particular group have similar behavior under given set of physical conditions.Any soil classification system must provide us with information about the probable engineering behaviour of a soil.The most commonly used properties for soil classification are

i) Grain size distribution
ii) Plasticity of soil
Read More

Mitigation of Soil Erosion with Jute Geotextile Aided by Vegetation Cover: Optimization of an Integrated Tactic for Sustainable Soil Conservation System (SSCS)
By Md Minhaz Mahmud, Nazmul Huda Chowdhury, Md Manjur Elahi, Md Hasanur Rashid, Md Kamrul Hasan
Khulna University of Engineering & Technology(KUET), Khulna, Bangladesh

Abstract
Degradation of soil considered as one of the foremost vulnerability and global threats nowadays not only for agricultural production and food security, but also for the environmental challenges related to watershed protection, disaster management, bio-diversity conservation, sustainable management of natural resources and climate change, furthermore, complication in Civil engineering. In Bangladesh where arable lands are less than necessary, certainly susceptible to severe erosion due to rainfall and flood, particularly when poor agricultural methods are used or preventive measures are not taken. Implementation of Jute Geotextiles (JGT) aided by native vegetation cover was investigated intended to design a sustainable and low cost tactic at Beel Dakatia through the entire year of 2009. Prime consequences were that erosion, moisture content and runoff are likely to be considerably impacted by rainfall intensity, soil surface slope; additionally, combined presence of JGT and vegetation cover reduced rate of erosion about 95% and runoff about 70% with respect to bare plots. Hence, play noteworthy role to conserve soil and stabilize the slope as well and mitigate susceptibility to degradation.

Keywords : Soil Protection, Jute Geotextiles (JGT), Watershed Management, Renewable Natural Resource, Disaster Management, Soil Strength.
Read More

In the past, it was believed that the formation of frost heave was related to the volumetric expansion of soil water which changed from liquid state to solid state. However, the increase of volume of changes in states for water at zero degree Celsius is only about 9% and the observed heaving is far more than this quantum.

In fact, the mechanism of frost heave is best explained by the formation of ice lenses. In cold weather, ice lenses develop in the freezing zone in soils where there is an adequate supply of soil water. Soil particles are surrounded by a film of water which separates the soil particles from ice lenses. The moisture adhered to soil particles gets absorbed to the ice lenses on top of the soils and in turn water is obtained from other soil pores to replenish the loss of water to ice lenses. This process continues and results in pushing up of soils on top of the lenses and subsequently the formation of frost heave.

This question is taken from book named – A Self Learning Manual – Mastering Different Fields of Civil Engineering Works (VC-Q-A-Method) by Vincent T. H. CHU.

During the construction of shotcrete, it is aimed at gunning the full thickness in one single operation and this helps to reduce the occurrence of possible delamination and formation of planes of weakness. Moreover, the nozzles should be held about 0.6m to 1.8m from the surface and normal to the receiving surface. The reason of gunning perpendicular to the receiving surface is to avoid the possible rebound and rolling resultingfrom gunning at an angle deviated from the perpendicular. The rolled shotcrete creates a non-uniform surface which serves to trap overspray and shotcrete resulting from the rebounding action. This is undesirable because of the wastage of materials and the generation of uneven and rough surface

This question is taken from book named – A Self Learning Manual – Mastering Different Fields of Civil Engineering Works (VC-Q-A-Method) by Vincent T. H. CHU.

For the construction of diaphragm walls, bentonite slurry is commonly used to form a filter cake on walls of trenches to support earth pressure. The use of bentonite solely is based on its thixotrophic gel viscosity to provide support.

Though the cost of polymer is generally more expensive than bentonite, the use of polymer is increasing because polymer is generally infinitely re-usable and very small amount of polymer is normally required for construction works. The disposal cost of bentonite is quite high while the disposal of polymer can be readily conducted by adding agglomerator.

This question is taken from book named – A Self Learning Manual – Mastering Different Fields of Civil Engineering Works (VC-Q-A-Method) by Vincent T. H. CHU.

The factor of safety for the embankment constructing on soft clay is minimum at the end of construction. After that consolidation takes place, thereby increasing the shear strength of foundation soils. Reinforcement is normally introduced to maintain the stability owing to the following reasons:

(i) The reinforcement at the clay surface, which is capable of carrying tensile forces, generates shear stresses to resist the lateral deformation of clay and improves its bearing capacity.

(ii) The reinforcement could also hold in equilibrium the lateral trust developed by the fill above so that it reduces the stresses which tends to cause failure of clay foundation.

(iii) The reinforcement has a tendency to drive the failure mechanism deeper in the soft clay, which should possess higher shear strength because its strength generally increases with depth.

This question is taken from book named – A Self Learning Manual – Mastering Different Fields of Civil Engineering Works (VC-Q-A-Method) by Vincent T. H. CHU.