By
D.Ishihara, H.Yamada, H.Katsuchi, and E.Sasaki
Yokohama National University
Abstract
There are plans of constructing bridges longer span like Messina strait bridge. This trend causes the necessity of discussing on the problems of instability analysis such as lateral-torsional buckling. However, lateral torsional buckling analysis of long span bridge is not sufficiently taken yet. For that reason, we apply the Abaqus/Standard to solve the high nonlinear problem. The analysis object is Akashi-kaikyo Bridge which is the longest bridge in the world. This paper presents how to analyze the lateral-torsional buckling of long span bridge applying wind load.
Keywords
Lateral Torsional Buckling, Suspension Bridge, Aerodynamics
Introduction
By now, a lot of long span suspension bridges have built and their lengths keep growing. As a result, their girder stiffness is relatively reduced and their strengths for wind force are also decreasing. Therefore, numerous futter analysis and experiments were executed. On the other hand, it is as well as important to investigate the lateral torsional buckling strengths of suspension bridges, but the investigations have never been made for decades. Certainly, we just use Hirai-Okauchi formulation that was proposed around 60’s to confirm the stability against the problem. It contains a theoretical equation and ideal boundary conditions so the application of the formulation is limited. Therefore, the need of modern examination of lateral torsional buckling of suspension bridge is increasing. A long span suspension bridge shows quite nonlinear behavior and shows non linearity when its initial condition and wind load are applied. Therefore it needs some techniques. We present the way of modeling bridges using the structural elements and making initial conditions under gravity. After this we present how to analyze the lateral-torsional buckling of long span bridge applying wind load. The wind load is calculated by the static coefficient of wind force. Finally, the result is showed and the conclusion is presented.
The main background of this problem and the procedure of the analysis are introduced in this chapter. The main topic of this analysis is a lateral torsional buckling and large deformation analysis of suspension bridge.
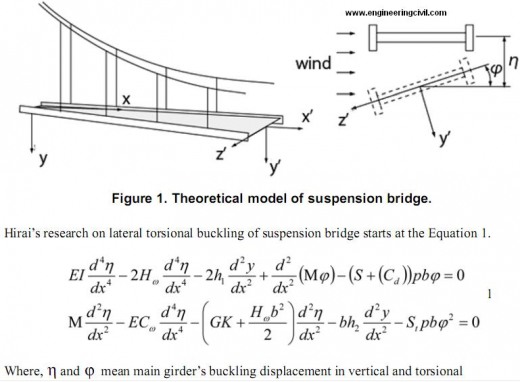
Hirai-Okauchi formulation
Lateral torsional buckling is critical for structures and can lead suddenly collapse of them. Previous research was conducted by Hirai(Hirai 1942) and Okauchi (Okauchi 1967). The main theory of their theory is showed as follows.
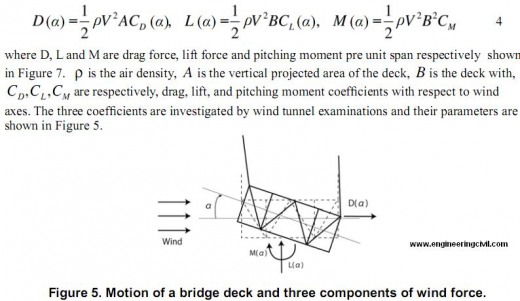
displacements, respectively. EI,GK,ECw are bending stiffness, torsional stiffness and bending torsional stiffness, respectively. Hw is tension force of main cable applying the dead load and M is the moment of horizontal component occurred by drag force. CD is a coefficient of drag,S and St represent the gradient of lift force and gradient of pitching moment. h1 h2 indicate the increment of cable tension caused by the deformation of lateral torsional buckling and each of them can be calculated by the following equations.
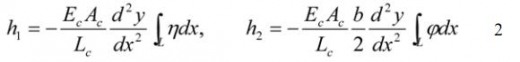
Where, EcAc is the cable’s stiffness, and right side of integration is applied for whole length of the suspension bridge. y is the vertical coordinate of cable before deformation. Hirai added the inertia term in Equation 1 and investigated on the stability criteria of structures by arranging the multi-coordinate vibration equation. In these investigations, it was found that the criteria is the same of the one of lateral torsional buckling. The importance of the problem of lateral torsional buckling was emphasized at that time. The critical wind load equation is
Because of the assumed boundary condition, the application of this equation is restricted to the single span suspension bridges. The application to the multi spans bridge and the different boundary conditions should have a problem. And also in the Equation 3, the transition of wind load to cable is not considered. As the pitching moment is the main component of lateral torsional buckling, the transition of wind load must had been considered in order to increase the accuracy of the equation.
These assumptions and ignorance should be removed in the modern analysis, because civil engineer should not rely on such a restriction of old theory but rely on comprehensive design method like Finite Element Method. In this study, the complicate FEM model was build and the above assumption and ignorance are eliminated. Therefore our study must be important to design the future bridges.
Target structure
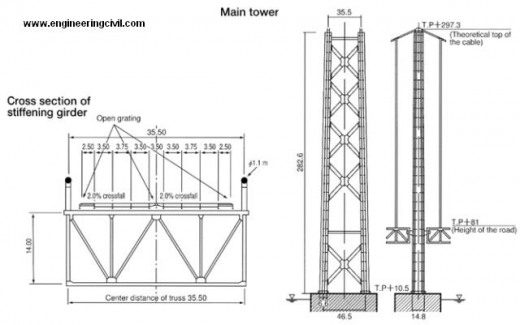
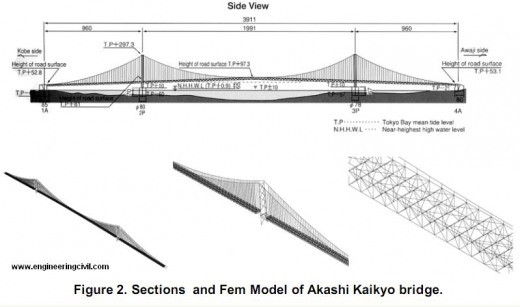
The application of large deformation and lateral torsional buckling analyses to long span suspension bridges are followed. One object of the analysis is Akashi Kaikyo Bridge; its center span is 1991m and is the longest in the world. The model is shown in Figure 2. In addition, we assembled the model of more lateral torsional buckling sensitive suspension bridge; the vertical brace made wider twice than the original Akashi Kaikyo Bridge. The two models are the objects of this chapter and we describe the details of them and the procedure of analysis.
Akashi Kaikyo bridge
Akashi Kaikyo bridge was completed in 1998 and is the world’s longest bridge. The main span is 1991 meters and the bridge has the stiffening truss girder. The outlines and some sections are showed in Figure 2.
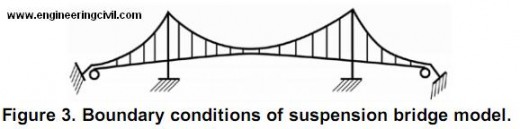
The main girder and tower are assigned beam element(B31H). The main cable and hanger cable are assigned truss element (T3D2H). The boundary conditions are showed in Figure 3. The towers and cable end are fixed, the girder ends are free in bridge direction (U1) but other degrees of freedom are fixed.
Simulated model of suspension bridge stiffened horizontally
An another analysis was performed in this study. The main point of this analysis is to investigate how will act the simulated model of suspension bridge stiffened horizontally against wind force. The suspension bridge model was modifed by increasing the stiffness of upper and lower chords by widening the width of elements. The upper and lower chord’s width was made twice as wide as Akashi Kaikyo model. The drawing of model is shown in Figure 3.
Except for the width of upper and lower chords modification, other parameters are all the same such as material, coordinates, and wind load.
Analysis procedure
The analysis procedure can be described as; bridges were applied the gravity at a first step, and bridges were applied the wind load at a second step. Each steps have high non linearity, which required the stabilization of damping factor. These details will be described afterward.
Gravity equilibrium
At a frst step, suspension bridges should be in equilibrium under gravity. While this step the models are applied with gravity load, and deforms as the number of increment is increasing. The deformation is so large that the normal static analysis cannot complete solving the step. Therefore, in this step, the damping factor was added to accomplish the analysis. This option can be written,
*Static, stabilize=4e-09
01, 1., 1e-40, 1. 0.
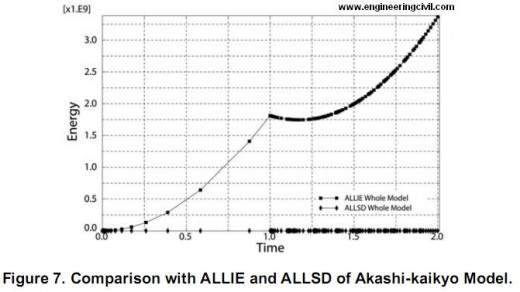
Of course, if the damping factor was added, the additional energy will act as factor which make analysis less accurate. Consequently, the comparison of ALLIE (total internal energy of structure) and ALLSD (total energy by damping factor) must be done. The comparison is done in chapter 5.
Applying Wind load
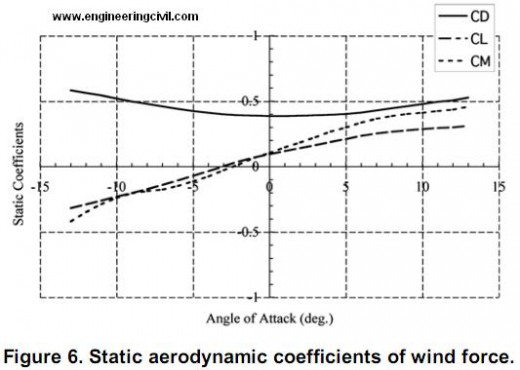
In the second step, the wind load is applied to the model. The three components of windfoce;pitching moment, drag force, and lift force are applied to elements. Each component is shown in Figure 7. The components of wind forces per unit span action on the deformed deck can be written,
The aerodynamic force applied to the wind-projected elements, which reflect the situation that the wind flows from one side horizontally. The magnitudes of wind forces are calculated by the Equation 4 and are applied after static analysis under gravity.
Analysis results and considerations
Gravity analysis
In the first step, the energy by damping factor should be much less than the internal energy, as previously mentioned. The comparisons of these factor are shown in Figure 6 and Figure 7. These figures show that the additional energy by damping factor is sufficiently less than the internal energy of structure. We can conclude that the effect of additional damping factor is well ignorable.
Analysis on the behaviors under aerodynamic forces.
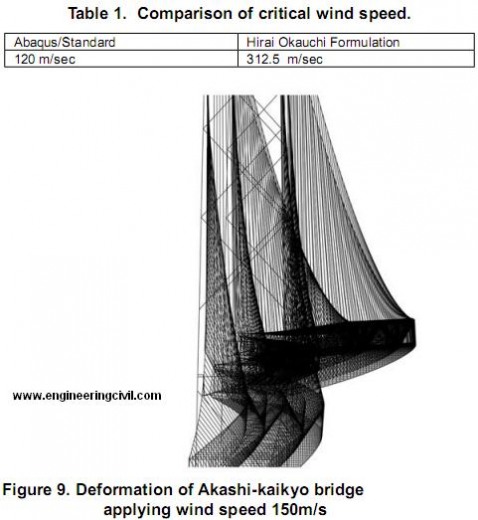
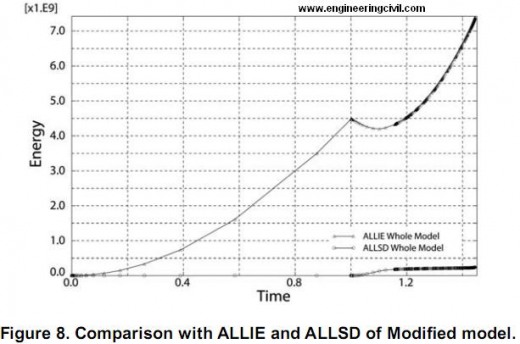
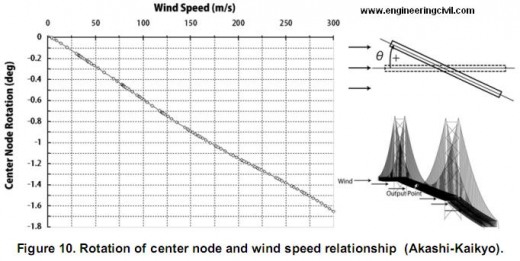
The large deformation analysis was done after under gravity analysis. The deformation figure and the relationship of rotational-displacement and wind speed are shown Figure 9 and Figure 10. Figure 9 shows the gradient increase of rotation of center node. The result represents the fact that the Akashi-Kaikyo Bridge doesn’t have the possibility of lateral torsional buckling but large deformation. If lateral torsional buckling occurs, the rotational displacement will increase suddenly, but this analysis doesn’t show such action. The reason of this is probably the suspension bridge’s stiffness of horizontal component is not greater than other stiffness components. While the simple beam analysis, the direction of applying load is the strong axes of the structure, but this suspension bridge is applied wind force horizontally and its horizontal stiffness is not so much strong.
On the other hand, the modified model’s behavior was different. Figure 10 shows the rotational displacement – wind speed relationship. It includes the lateral torsional behavior character that the rotational displacement increase suddenly.
Considerations
In the problem of lateral torsional buckling, the balance of stiffness is very important. If the horizontal stiffness is small compared with other directional stiffness, the structure occurs only large deformation and if the one is large over some point, the structure occurs lateral torsional buckling.
In addition to the described analysis, we calculated the critical wind speed by Hirai Okauchi formulation. The parameters are shown in Table 1. This table represents the great reduction of critical wind speed. This means the previous theory is in danger side judgment.
Conclusions
In this paper lateral torsional buckling analysis by utilizing the Abaqus standard was demonstrated. The balance of horizontal stiffness is very important ant the over stiffness of that leads the structure lateral torsional buckling. However, it should be noted that the analysis’ results need more verification such as experiments: wind tunnel test. For continuing research, the critical balance of stiffness and other real suspension bridge analysis should be classified.
References
1. Memon Bashir-Ahmed, et al, “Arc-length technique for nonlinear fnite element analysis,” Journal of Zhejiang University SCIENCE Vol.5(5), pp. 618-628
2. Virote Boonyapinyo,T. Miyata, H. Yamada, “Nonlinear buckling instability analysis of long-span cable-stayedbridges under displacement-dependent wind load,” Journal of structural engineering, Vol.39A P923-935, 1993.
3. M.A.Crisfeld, “A Fast Incremental/Iterative Solution Procedure that Handles “Snap-Through””, Computers & Structures Vol.13, pp 55-62.
4. M.A.Crisfeld, “Snap-Through and Snap-Back Response in Concrete Structures and the Dangers of Under-Integration,” International Journal for Numerical Methods in Engineering,Vol. 22 pp. 751-767
5. M.Fafard , B.Massicotte, “Geometrical Interpretation of the Arc-Length Method”, Computers & Structures Vol.46, No.4, pp 603-615.
6. A.Hirai, “The stability of suspension bridges against torsional vibration,” Journal of Japan Society of Civil Engineers summery vol.28 pp 769-786, 1942.
7. A.Hirai, Y.Fujisawa “The effects of frequency of wind load to the elastic stability of suspension bridges” Journal of Japan Society of Civil Engineers summery vol.21 pp 85-1, 85-2,1966.
8. A.Hirai, H.Takema, “Lateral torsional buckling of suspension bridge under horizontal wind load” Journal of Japan Society of Civil Engineers summery vol.13 pp 19-20,1958.
9. Japan society of civil engineering and Honsyu-shikoku bridges technological workshop, “Report of honsyu-shikoku bridge technological survey appendix.1,”,1967.
10. J.H.Kweon, C.S.Hong , “An Improved Arc-Length Method for Postbuckling Analysis of Composite Cylindrical Panels,” Computers & Structures Vol. 53, No. 3, pp 541-549.
11. W.F.Lam, C.T.Morley, “Arc-length Method for Passing Limit Points in Structural Calculation” Journal of structural engineering Vol.118 No.1 P169-185.
12. Long pillar workshop, “Handbook of elastic stability,” Corona Publishing, 1960.
13. Mark J. Silver, et al, “Modeling of Snap-Back Bending Response of Doubly Slit Cylindrical Shells,” Structural Dynamics & Materials Conference, AIAA2004-1820.
14. K.Okauchi, K.Nemoto, “Lateral torsional buckling of suspension bridges under wind pressure,” Journal of Japan Society of Civil Engineers summery vol.22 pp 136-1, 136-4, 1967.
15. G.Powell, J.Simons, “Improved Iteration Strategy for Nonlinear Structures”, International Journal for Numerical Methods in Engineering,Vol17 PP1455-1467.
16. E.RAMM, “Strategies for Tracing Nonlinear Response Near Limit Points Non-linear finite element analysis in structural mechanics”, Springer-Verlag, New York.
17. E.Riks, “The Application of Newton’s Method to the Problem of Elastic Stability”, Journal of Applied Mechanics , Vol39 PP1060-1065.
18. E.Riks, “An Incremental Approach to the Solution of Snapping and Buckling Problem,” International Journal if Solids Structures, Vol.15, pp529-551.
19. H.Takema, K.Okauchi, “Lateral torsional buckling of suspension bridges under wind pressure,” Conference of bridge and structure workshop vol.11 ppp26-39, 1964.
20. Timocshenko, Gere, “Theory of elastic stability,” McGrawHill, 1961.
We are thankful to Sir Matthew Ladzinski for submitting this report to engineeringcivil.com and also granting us rights to publish it on web. This report will help all civil engineers study the Lateral Torsional Buckling of Long Span Suspension Bridge.
If you have a query, you can ask a question here.



its nice……..
ITS VERY NICE AND ADVANTAGEOUS
please send the abbrevations for ALLIE and ALLSD. Plz send me urgent.
PLEASE SEND ME ESTIMATE OF BRIDGES