Analysis and Design Of 2-D Tubular Frame Using USFOS Modeling by
SOURADEEP GUPTA
Department of Civil and Environmental Engineering
National University Of Singapore
Abstract:
USFOS is the analytical tool for predicting both the resistance of structures subject to accidental loads and the residual strength of damaged structures after such loads. It is based on finite element modeling. USFOS covers static collapse analysis, non-linear time series dynamic analysis as well as eigenvalue analysis of typically jackets, jack-ups, topsides and floaters. Primarily the purpose of this paper is to analyze two types of 2-D offshore frame and study the progressive collapse mechanism in these two frames due to different load combinations along X-axis and Y-axis. First the boundary conditions were fixed for the vertical members using USFOS modeling and they were tested for collapse under four different load combinations. Differences in behavior of two frames have been studied and different brace-chord sizes have been fixed. This type of analysis is useful to test if an offshore jacket with some specified size can stand the load coming on it from waves, wind or impact of ships. By utilizing the inherent redundancy found in most offshore structures the progressive collapse limit state can be used to design for accidental damage or extreme loads. Whereas in traditional elastic design redistribution of load is not normally considered. Collapse or plastic limit state design allows for local failure in yield or buckling and even partial collapse, provided the overall integrity of the structure is maintained. In short, plastic limit state design allows the designers to take advantage of any reserve capacity in the structure.
Introduction
The elastic method of designing a structure depends on the elastic properties of steel. While designing a structure based on elastic property, strength of the steel till its yielding point is alone considered. But the strength of steel beyond the yielding point is not considered in elastic design. So the structure designed based on the elastic limit will be large and also not economical. But the plastic methodology of designing considers the ultimate strength of steel and hence the resulting structure will be smaller in size when compared to elastic design and also more economical. This method has its main application in the analysis of statically indeterminate framed structures. Plastic analysis and design can only be adopted if the material has a good duct ile property. The objective of this project is to correct and analyze the BOMEL 2D frame. Also to analyze K-Joint and X-Joint frames for various load cases.
Analysis of BOMEL 2-D Frame:
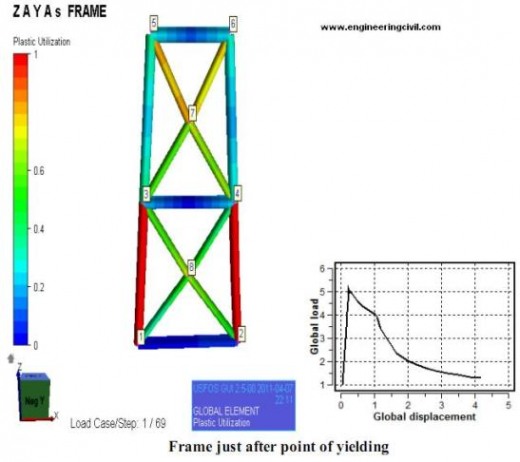
The objective of this analysis is to find the mistakes done in the modeling of Bomel 2D frame and to study it when using the rigid and MSL joint formulation. The figure shown below is the model of 2-D Bomel frame with its dimensions.
In the structural file the brace members of cross joint in top and bottom bay were modeled incorrectly (properties). After correcting the structural file, it was used with given model file and the structure was analysed for rigid and MSL joint formulation for two X joint. The Global Load Vs Displacement curve obtained in the analysis is shown in the figures below:
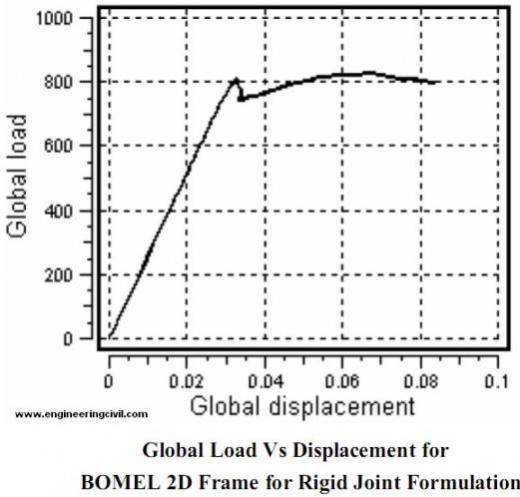
The theoretical load vs displacement curve was shown in the figure below. It can be inferred that after reaching the yielding point frame can still take load which is due to the residual strength of the MSL joint formulation.
From the two curves above it can be clearly seen that there is a sudden drop in load value in rigid curve joint when compared to that of MSL joint curve. The MSL joint formulation better suits the theoretical curve than rigid joint curve. This is mainly due to two reasons. First the increased load carrying capacity of MSL joint formulation is due to better force distribution in the X joint. Second is due to the increased reserve strength in the MSL formulation when compared to rigid joint. The table given below shows the Global Load, displacement for the theoretical, rigid and MSL joint formulation.
| Study conducted | Global Load | Global displacement |
| From theoretical Graph | 700 | 50 |
| Rigid joint | 800 | 28 |
| MSL joint | 620 | 32 |
Table for Global Load –displacement for various joints
The above value shows that the rigid joint has a better joint capacity than MSL joint. However, the ultimate strength is more or less the same. Rigid joint failure is a buckling type and MSL joint formulation failure is a yielding type. The rigid joint achieved buckling with short displacements, while MSL joint can take same amount of load without buckling.
Analysis of 2D Frames:
Assumptions:
1. Analysis is done on a 2-D model frame. In USFOS, if a frame is designed as a 2-D model, then X represents the horizontal direction and Y represents the vertical direction.
2. Boundary condition was assumed to be fixed in all directions except free to rotate in Y-direction alone.
3. The joint were considered as rigid one
4. The material properties used in analyzing both the frames were constant.
E=200GPa and Yield Stress = 355MPa.
The frames which are going to be analyzed in this project are Type I and Type II.
Frame Dimensions: Height: 44m, Width: 14m, Batter: 1:12.
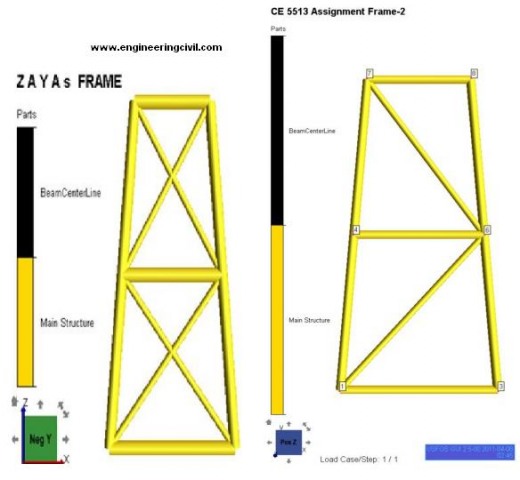
Frame Models in USFOS:
The pictures below show the model of Frame I and II with their nodal and element numbers. All the members are designed using Circular Hollow cross section (CHS). For the simplicity in design, only two geometries were considered. All Chord elements have the same diameter. thickness and in the same way all the brace elements have the same diameter and thickness. The material properties such as Elastic Modulus (200GPa) and Yield strength (275-355MPa) was considered as given in the project requirement.
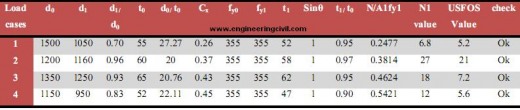
Different Load Cases for Frame II-X Joint:
Case1: When a load of 10MN is applied in X direction:
The member dimensions for this load case are 1500mm OD 55mm WT for the chord and 1050mm, 52mm WT for the brace members. Since the analysis is based on non linear analysis, incremental load, time step are carefully adjusted to get a reasonable load displacement curve. Various combinations of diameter thickness were used to generate a proper load versus displacement curve. Finally for the dimensions mentioned above a proper load displacement curve was obtained as shown in the figure below.
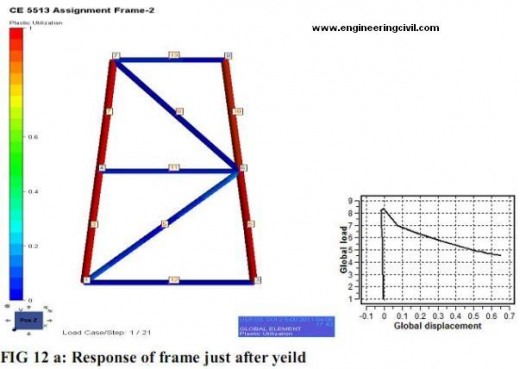
The above two figures shows the response of frame. Failure is first observed at a load of around 5.3 MN and appears in the form of plastic zone formation in the lower bay legs. With more displacement and not very much change in load carrying capacity the right lower leg buckles and simultaneously the braces also develop plasticity. But the left lower leg that also developed simultaneous plastic zone along with the right one does not show any sign of deformation. It testifies that more load is being carried by the right leg and the lower brace. The next frame shows the response of the frame at the maximum displacement as could be noted in the global load-displacement curve. Load factor at yield is 5.3 which implies it can carry a load of 53 MPa.
Case2: Load of 10MN applied in Y-Direction:
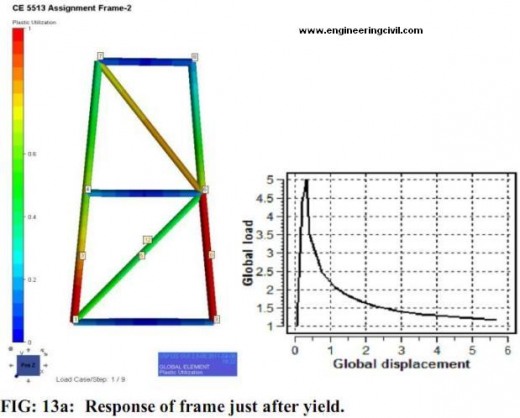
In this case, load of 10 MN is applied in Y-direction. As shown in the project requirement this load is separated into two 5MN and it is applied at the nodes 5 and 6. A number of trial run was conducted to determine a proper diameter and thickness and also to obtain a proper load versus displacement curve. After making several trial runs chord member with 1200mm OD and 60mm WT was taken. Brace dimensions was taken as 1160mm OD and 58mm WT. For this case the load is applied at node 5 and 6. As the load is application is directly above the chord members, the initial load carrying capacity depends on the chord strength. The ultimate load carried by the frame is about 21.5 MN without any plastic zone formation. Notable displacement has occurred at load beyond 21.5 MN where a sharp drop in load carrying capacity has been observed. Main cause is formation of plastic zone in the lower portion of the left leg with more displacement and with no drastic change in load carrying capacity. The top portion of the right leg bulges outside while the lower portion bulges in with buckling in the left lower leg as well. The left lower leg does not buckle after a certain limit (no displacement) but the plastic zone seems to be transferred to the brace. The response is illustrated in the figures below.
Case 3: Load applied in both directions (Px=2Py):
In this case the load is applied in both X and Y direction simultaneously. The load applied in the X-direction is at node 5 and it is equal to 0.66MPa. And at node 6, load of 0.33MPa is applied in Y-direction. As stated earlier various trial runs were conducted and the suitable member dimensions were found out. Chord dimensions are taken as 1350mm OD and 65mm WT. Brace members have a OD of 1250mm and 62mm WT. It is clear from the figures shown below that the chord member 6, 7 carries the load applied till the yielding point. The figure also proves that much of the load is carried by the chord members initially. Once the yielding point is reached, member 7 buckles and the X-joint (brace) members start to takes the load. The load distribution is linear from now on and the frame collapse slowly.
Case 4: Load applied in both directions (Px=0.5Py):
The load is applied in both the direction with 0.66MPa acting in Y-direction and 0.33MPa in X-direction. After careful investigation member dimensions for chord members was chosen as OD of 1150mm, WT of 52mm and the brace members was chosen as 950 OD , 47mmWT.
The loads are acting at the node points 5 and 6. The below figure shows the behavior of the frame at the time of yielding. It is clear that the chord members take most of the loads when compared to the brace members. In this case majority of the loads act at the node point 6 and so the member 7, 13 takes most of the load. First plastic hinge develops in right lower leg ( member 7) just above 10 MN. The peak value of load as recorded from global load displacement curve is 5.6 MN. The load carrying capacity decreases due to the formation of plastic zone in the top bay brace which causes buckling in the brace as well as in the top bay leg.
FRAME- I
Different Load Cases for Frame I:
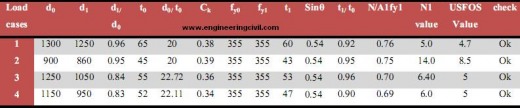
Case1: Load applied in X- direction:
In this case load of 10MPa is applied in X-direction. After various trail suitable member dimensions were chosen. Chord diameter was taken as 1300mm OD with 65mm WT and brace member have 1250mm OD with 60mm WT. The figure below shows the yielding of frame with global load displacement curve. It also shows that K-joint in the bottom area of the frame yield at the maximum load. On reaching a peak load of 4.7 units first plastic zone formation is noticed in element 6. More displacement is caused as buckling in member 6 takes place. Upon failure of member 6 considerable amount of load seems to be carried by 3,10 and 12. The response is illustrated in the figures below.
CASE 2: Load applied in Y direction:
A load of 10MPa was applied in Y- direction at node 7 and 8 for this case. The member dimensions are taken as 860mm OD, 43mm WT for chord member and 900mm OD, 45mm WT for brace members. At the point of yielding, the load is taken by the chord and joints at 4 and 6. This is shown in the figure below. Just after the yield displacement is observed due to buckling of member 6 and change of position of member 7. Major part of load is still endured by K-joint brace members. When first plastic zone was observed in the legs the brace members were well below their plastic limit. From the global load-displacement curve load factor of 8.5 is observed which implies the structure is able to carry load of 85 MPa.
Case 3: Load applied in both directions (Px=2Py):
In this case load is applied in both direction with 0.66MPa on X direction and 0.33MPa on y direction. The dimensions for chord members are 1240mm OD, 55mm WT and 1050mm OD, 53mm WT for brace. At yielding point, K-joint at node 6 fails and the member 6 starts to buckle followed by subsequent buckling of brace member 8 accompanied by more displacement. The Ultimate Load carrying capacity is about 5 times higher than the initial load applied. This can be seen in the figure below. Collapse of the frame commences with buckling of member 6 and 8. The member 8 buckles since the load applied in the X direction is greater than the load applied in Y-direction.
Case 4: Load applied in both direction (Px=0.5Py):
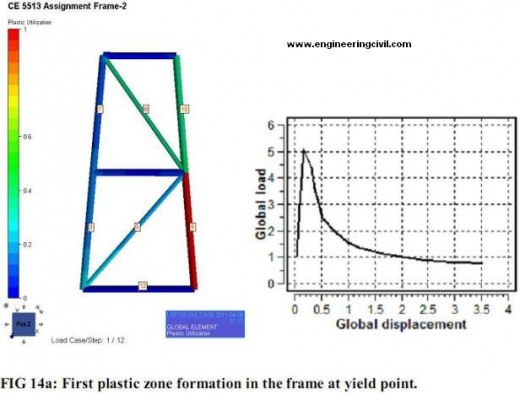
In this case loads are applied in both the direction simultaneously. The load applied in Ydirection at node 8 is larger compared to load applied in X-direction at node 7. The dimensions of the members selected are 1150mm OD, 52mm WT for the chord and 950 mm OD and 47mm WT for the brace. At maximum yielding point, joint at the node 6 fails and chord member 6 starts to buckle. This is the shown in the figure14 below. The maximum load carrying capacity for the frame designed is around 5 times higher when compared to applied load of 10MN. Fig 14 b shows the collapsed frame where the joint 6 fails. Stress near node1 also reaches plastic limit due to which member 3, 5 and 12 shows some plasticity near the edges.
Summary of member dimensions:
The table below gives the diameter and thickness of members for various load cases. The main criteria which is considered while designing is diameter to thickness ratio and it should be equal to or greater than 20(d/t=20). All the member diameter and thickness chosen were within the stipulated conditions. Summary table for frame II is displayed below.
| Load cases | Members | Diameter (mm) | Thickness(mm) |
| Load case 1 | Chord | 1300 | 65 |
| Brace | 1250 | 60 | |
| Load case 2 | Chord | 900 | 45 |
| Brace | 860 | 43 | |
| Load case 3 | Chord | 1240 | 55 |
| Brace | 1050 | 53 | |
| Load case 4 | Chord | 1150 | 52 |
| Brace | 950 | 47 |
Summary table for frame II:
| Load cases | Members | Diameter (mm) | Thickness(mm) |
| Load case 1 | Chord | 1500 | 55 |
| Brace | 1050 | 52 | |
| Load case 2 | Chord | 1200 | 60 |
| Brace | 1160 | 58 | |
| Load case 3 | Chord | 1350 | 65 |
| Brace | 1250 | 62 | |
| Load case 4 | Chord | 1150 | 52 |
| Brace | 900 | 47 |
Comparative study done on Two types of frames :
From analyzing four different load cases for both X-frame (frame II) and K-frame ( frame I) and going through load displacement curve we can clearly infer that load carrying capacity of the frame with K-joint falls suddenly when compared with X-joint frame. This may be because of the fact that initial load was being taken by the chord members and after reaching yield point it was transferred to the other brace member through joints. Also X-frame has more redundancy when compared to K-joint frame. For further illustration a table showing global load in case of both frames is presented below and a graphical representation is also shown.
|
Load Cases |
GLOBAL LOAD |
|
|
X-joint |
K-joint |
|
|
Load case 1 |
5.2 |
4.7 |
|
Load case 2 |
21 |
8.5 |
|
Load case 3 |
7.2 |
5 |
|
Load case 4 |
5.6 |
5 |
Analysis of joint strength using CIDECT curve:
The design strength of joint formulation was checked by comparing its values with theoretical CIDECT curve. The design strength values should be greater than theoretical values. X-joint: The following graph shows the theoretical CIDECT curve for X-joint:
K-joint:
The graph below shows the theoretical CIDECT curve for K –joint (assuming a gap function of g’ = 2).
The table shows the check made on the modeled frame using CIDECT curve.
Conclusions:
Study on the difference between modeling of Joint by rigid joint formulation and cross joint formulation was done by BOMEL 2D frame (one with K-joint and other with X-joint) by correcting the model file. And also two 2D frames have been modeled by using USFOS and four different load cases were tried by altering member dimensions and studying the global load-displacement curve in each case. The analysis was done by carefully noting the behavior of each frame member under load conditions. Some of the key points noted during the analysis are presented below.
A) Failure of rigid joint occurs by buckling (chord in maximum case and it also depends upon the direction of load applied).In case of MSL joint yield point is first reached and the load carried is distributed to other members. So sudden collapse does not occur in frames with MSL joint assumption.
B) Comparing the joint strength it is seen that strength of rigid joint is more than MSL joint. But the maximum load carrying capacity is almost same in both cases.
C) When comparing frame II and frame I it is seen that X-joint frame ( frame II) carries more load than K-joint frame ( frame II). This result might be due to the fact that in case of X-joint load is transferred to the other members smoothly and collapse does not occur all of a sudden.
D) I carried out one study on frame II by removing the middle horizontal member which seems to be redundant though it was outside the scope of what has been asked in the assignment. It has been found that due to the presence of that member the post ultimate load carrying capacity of the frame is increased by 15-17 % (depending upon member dimension). It would add to the self weight of the structure but the overall frame response improves by the addition of the member. The peak load carried by the frame may seem to be the same but the drop in strength is larger for the frame without the middle horizontal member. Post ultimate strength is larger in case where middle horizontal member is present.
E) By keeping the chord diameter and brace diameter ratio almost close to unity a better frame response has been observed in every occasion.
F) I tried to analyze the frame response by adjusting diameter and thickness of members. I noticed that the strength of member or capacity of any member depends largely on thickness of pipe than on the diameter.
SAMPLE SET OF USFOS PROGRAM.
Click to check the model file
Click to check the Structural file
References:
[1] J. Wardenier, Y. Kurobane, J.A.Packer, G.J. Vander Vegte,X.L Zhao. Design Guide for circular hollow section ( CHS) joint under predominantly static loading. CIDECT, 2008.
[2] Structural hollow ( MSH)- circular, square, rectangular. VALLOUREC & MANNESMANN TUBES.
[3] Ultimate strength Performance of Offshore structural Engineering. Offshore Technology Report, Health and safety executive, March, 2000.
We are thankful to Sir Souradeep Gupta, National University of Singapore for publishing his research work on “Analysis and Design Of 2-D Tubular Frame Using USFOS Modeling” here on engineeringcivil.com.
If you have a query, you can ask a question here.