By
Mr.Abhinandan R.Gupta
Asst.Prof, Dept. Of Civil Engg.
COET,Akola
ABSTRACT:
With the urge for sustainable, durable and economical construction various methods for designing, developing and constructing structures right from Class I structures like Important service and community structures – Power plants, Reservoirs, Health care centers, Airports to ordinary structures have been developed rapidly in the last few decades.
Along with these construction techniques the reliability of present or proposed structure is determined with various analysis and designing methods for parameters under consideration. One such reliable and effective method is Finite element Method. FEM even if complex and hard for manual analysis but is one of the most efficient method for software programming.FEM method works effectively even for complex structure with efficient results or outcomes.
Such complex structure can be defined complex because of their geometrical shape, composition or development of stresses within them. These strange parameters make many of analysis and designing classical method less efficient as they are developed for conventional structures or cases. One of the example is Circular Presstressing structure like water tank, “Prestressed” word itself makes designing process unusual along with analyzing it for stress and bending moment pattern for same structure before and after designing.
Over here the analysis and designing is done using Finite Element Method for Pestressed Water Tank. For considered grid pattern and assumptions made the results for stress and Bending moment are checked with the analysis and designing method of Indian standard code of Practice: 1343-1980, 3370-III,IV,1965. The aim of the paper is to study the stress pattern for circular prestressed water tank, designing it based on FEM results and to check Finite Element Methods applicability for such unusual construction method. Outcomes obtained after designing and analysis by FEM marked its high efficiency for such structures too.
INTRODUCTION
The finite element method is a numerical analysis technique for obtaining approximate solutions to a wide variety of engineering problems. Although originally developed to study stresses in complex airframe structures, it has since been extended and applied to the broad field of continuum mechanics. Because of its diversity and flexibility as an analysis tool, it is receiving much attention in engineering schools and in industry. In more and more engineering situations today, we find that it is necessary to obtain approximate numerical solutions to problems rather than exact closed-form solutions. Several approximate numerical analysis methods have evolved over the years; a commonly used method is the finite difference scheme. The familiar finite difference model of a problem gives a point wise approximation to the governing equations.
Unlike the finite difference method, which envisions the solution region as an array of grid points, the finite element method envisions the solution region as built up of many small, interconnected sub regions or elements. A finite element model of a problem gives a piecewise approximation to the governing equations Since these elements can be put together in a variety of ways, they can be used to represent exceedingly complex shapes.
Thus Prestressed Concrete water tank is chosen for analysis and design by FEM, since Prestress water tank can be considered as a complex structure because of its construction methodology . Basically Prestressing means inducing the stresses in body or structure of opposite nature. In other words it means that developing the opposite nature stress in initial stage only so as to resist stress developed in working conditions. We are just nullifying the acting and reacting forces or actions. In prestessing we induce compressive forces or stresses in concrete material so that if tensile forces are acting on it the compressive stresses induced initially will nullify total stress effect, keeping structure safe and durable.
SCOPE:
Over here the study is done for Prestress water tank resting on ground .Analysis is done for Stresses, Hoop Tension and Bending moment at various level and faces of tanks as per Grid formation methodology of Finite Element Method.
DESIGNING PHILOSOPHY :
In a continuum problem of any dimension the field variable like tank, possesses infinitely many values because it is a function of each generic point in the body or solution region. Consequently, the problem is one with an infinite number of unknowns. The finite element discretization procedures reduce the problem to one of a finite number of unknowns by dividing the solution region into elements and by expressing the unknown field variable in terms of assumed approximating functions within each element. The approximating functions (sometimes called interpolation functions) are defined in terms of the values of the field variables at specified points called nodes or nodal points. Nodes usually lie on the element boundaries where adjacent elements are connected. In addition to boundary nodes, an element may also have a few interior nodes. The nodal values of the field variable and the interpolation functions for the elements completely define the behavior of the field variable within the elements. For the finite element representation of a problem the nodal values of the field variable become the unknowns. Once these unknowns are found, the interpolation functions define the field variable throughout the assemblage of elements.
There are basically three different approaches.
1) To obtaining element properties is called the direct approach because its origin is traceable to the direct stiffness method of structural analysis. The direct approach suggests the need for matrix in dealing with the finite element equations. Element properties obtained by the direct approach can also be determined by the variational approach.
2) The variational approach relies on the calculus of variations and involves extremizing a functional.
3) A third and even more versatile approach to deriving element properties has its basis in mathematics and is known as the weighted residuals approach.
In this paper Direct approach is taken into consideration.
4. Steps in Analysis done:
A. Discretize the Continuum. The first step is to divide the continuum or solution region into elements. A variety of element shapes) may be used, and different element shapes may be employed in the same solution region. In this problem the discretizations is done in the form of 2-D strip with Integral limit 0 to H at base of tank. Since the integral is taken into account each element is 8 noded with interval of H/10 along Y- axis and t along X – axis. Accuracy and approximation depends upon the way and finesse of grid.
B. Select Interpolation Functions. The next step is to assign nodes to each element and then choose the interpolation function to represent the variation of the field variable over the element. The field variable may be a scalar, a vector.The degree of the polynomial chosen depends on the number of nodes assigned to the element, the nature and number of unknowns at each node, and certain continuity requirements imposed at the nodes and along the element boundaries.

C. Find the Element Properties. Once the finite element model has been established (that is, once the elements and their interpolation functions have been selected), we are ready to determine the matrix equations expressing the properties of the individual elements. Formula below shows the state of stress in an elemental volume of a body under a load. It is defined in terms of three normal stress components sx, sy, and sz and three shear stress components txy, tyz, and tzx. The corresponding strain components are three normal strains ex, ey, and ez and three shear strains gxy, gyz, and gzx. These strain components are related to the displacement components u, v, and w at a point as follows:

D. Assemble the Element Properties to Obtain the System Equations. To find the properties of the overall system modeled by the network of elements we must “assemble” all the element properties. In other words, we combine the matrix equations expressing the behavior of the elements and form the matrix equations expressing the behavior of the entire system.

E. Impose the Boundary Conditions. Before the system equations are ready for solution they must be modified to account for the boundary conditions of the problem. At this stage we impose known nodal values of the dependent variables or nodal loads. The potential energy of the external load in the deformed configuration of the element is written as In Equation {Q_} represents concentrated loads at nodes and {q} the distributed loads per unit area. Substituting for {f }T from Equation one obtains

F. Solve the System Equations. The assembly process gives a set of simultaneous equations that we solve to obtain the unknown nodal values of the problem. If the problem describes steady or equilibrium behavior, then we must solve a set of linear or nonlinear algebraic equations.
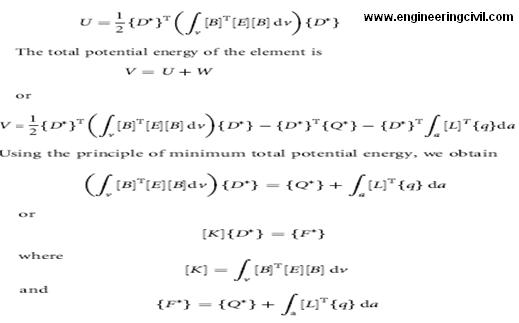
5. RESULTS & DISCUSSION
Example was taken under consideration with Dimensions and material grade as follows-
Cylindrical Prestressed water tank – Rigid base resting on Gound :
Intenal Diameter: 30 m
Avg. wall thickness: 150 mm
Height of tank: 7.35 m
Loss ratio ?: 0.75
Permissible comp. stress at tanspher: 13 N/mm2
Min. comp. stress in working condition: 1 N/mm2
Cubic strength of Conc: 40 N/mm2
1.) Values obtained using formula given in IS 3370-IV, table no. 9
Hoop tension Nd= Coefficient x wHR.
H2 / Dt = (7.35)2 / (30 x 0.15) = 12.00
Density of fluid (water) W= 9810
Moment = Coefficient x w H3 Kgm/m
2) Values of FEM is done as per the Formula and programme made for the element and structure.
Initally the values of Displacemnt is obtained, further integrating double we get Bending Moment , triple integration gives value of Force i.e Hoop tension .
| Height Level | Value of Hoop tension and Bending Moment as per IS-3370-IV | Value of Hoop tension and Bending Moment as per FEM analysis | ||
| Hoop tension Nd (N/m) | Moment M (N-m) | Hoop tension Nd (N/m) | Moment M (N-m) | |
|
0.0 H |
– 5407.75 |
0.000 |
-5378.00 |
0.001 |
|
0.1 H |
1258927.11 |
-389.521 |
1258911.15 |
-382.331 |
|
0.2 H |
218473.60 |
389.521 |
218470.79 |
385.427 |
|
0.3 H |
337444.38 |
779.042 |
337447.89 |
781.127 |
|
0.4 H |
463986.02 |
1168.563 |
463984.00 |
1168.500 |
|
0.5 H |
587283.00 |
5063.774 |
587279.11 |
5060.997 |
|
0.6 H |
679214.97 |
8958.986 |
679214.82 |
8955.253 |
|
0.7 H |
684622.73 |
10127.54 |
684599.41 |
10129.53 |
|
0.8 H |
534286.93 |
-1947.605 |
534290.57 |
-1950.213 |
|
0.9 H |
228207.5 |
-40510.197 |
228200.01 |
-40509.200 |
6. CONCLUSION:
Results of the analysis done using Finite Element Method gives approximately same values as per the values obtained by classical method given in IS- 3370 Part IV.
Since freedom and flexibility to choose the grid pattern highly affects the accuracy of values obtained.
Over here the mesh was not considered to dense, however more appropriate answers can be achieved by developing fine mesh.
Since unusual geometrical shape and distinct construction methodology structure can be analyse easily as in example above for Prestressed tank, applicability of Finite element Method proves to be effective and efficient
FUTURE SCOPE
Same structure can be analyse by FEM by forming various grid pattern considering 2-D strip element, Axisymmetric –Axiloaded ring element, 3-D parallelepiped element or Shell element. Along with this analysis can be done for composite structure with different material property which will prove to be challenging.
REFERENCES
1. D. A. Anderson, J. C. Tannehill, and R. H. Pletcher, Computational Fluid Mechanics and Heat Transfer, Hemisphere, Washington, DC, 1984.
2. F. J. Rizzo, “An Integral Equation Approach to Boundary Value Problems of Classical Elastostatics,” Q. Appl. Math., Vol. 25, 1967, pp. 83–95.
3. F. J. Rizzo and D. J. Shippy, “An Advanced Boundary Integral Equation Method for Three-Dimensional Thermoelasticity,” Int. J. Appl. Mech., Vol. 11, 1977, pp. 1753–1790.
4. C. Brebbia, J. C. F. Telles, and L. C. Wrobel, Boundary Element Technique, Springer-Verlag, Berlin, 1984.
5. R. P. Banaugh and W. Goldsmith, “Diffraction of Steady Acoustic Waves by Surfaces of Arbitrary Shape,” J. Acoust. Soc. Am., Vol. 35, No. 10, 1963, pp. 1590.
6. R. W. Clough, “The Finite Element Method in Plane Stress Analysis,” Proceedings of 2nd ASCE Conference on Electronic Computation, Pittsburgh, PA, September 8–9, 1960.
7. R. Courant, “Variational Methods for the Solutions of Problems of Equilibrium and Vibrations,” Bull. Am. Math. Soc., Vol. 49, 1943, pp. 1–23.
8. J. Greenstadt, “On the Reduction of Continuous Problems to Discrete Form,” IBM J. Res. Dev., Vol. 3, 1959, pp. 355–363.
9. P. M. Morse and H. Feshback, Methods of Theoretical Physics, McGraw-Hill, New York, 1953, Section 9.4.
10. W. Prager and J. L. Synge, “Approximation in Elasticity Based on the Concept of Function Space,” Q. Appl. Math., Vol. 5, 1947, pp. 241–269.
11. J. L. Synge, “Triangulation in the Hypercircle Method for Plane Problems,” Proc. R. Irish Acad., Vol. 54A21, 1952.
12. A. Hrenikoff, “Solution of Problems in Elasticity by the Framework Method,” J. Appl. Mech., Vol. 8, 1941, pp. 169–175.
13. D. McHenry, “A Lattice Analogy for the Solution of Plane Stress Problems,” J. Inst. Civ. Eng., Vol. 21, 1943, pp. 59–82.
14. N. M. Newmark, in Numerical Methods of Analysis in Engineering, L. E. Grinter (ed.), Macmillan, New York, 1949.
15. G. Kron, “Tensorial Analysis and Equivalent Circuits of Elastic Structures,” J. Franklin Inst., Vol. 238, No. 6, December 1944, pp. 400–442.
16. G. Kron, “Equivalent Circuits of the Elastic Field,” J. Appl. Mech., Vol. 66, 1944, pp. A-149 to A-161.
17. J. H. Argyris, “Energy Theorems and Structural Analysis,” Aircraft Eng., Vol. 26, October-November 1954, pp. 347–356, 383–387, 394.
18. J. H. Argyris, “Energy Theorems and Structural Analysis,” Aircraft Eng., Vol. 27, February-March-April-May 1955, pp. 42–58, 80–94, 125–134, 145–158.
19. J. H. Argyris, “The Matrix Theory of Statics” (in German), Ingenieur Archiv, Vol. 25, 1957, pp. 174–192.
20. J. H. Argyris, “The Analysis of Fuselages of Arbitrary Cross-Section and Taper,”
Aircraft Eng., Vol. 31, 1959, pp. 62–74, 101–112, 133–143, 169–180, 192–203, 244–256, 272–283.
21. J. H. Argyris and S. Kelsey, Energy Theorems and Structural Analysis, Butterworth, London, 1960.
We at engineeringcivil.com are thankful to Sir Abhinandan R. Gupta for submitting this research paper on “Design Of Prestressed Shell type Strucutre using Finite Element Method” to us. We are hopeful that this will be of great use to other civil engineers who are looking forward to conduct a research in this field.
If you have a query, you can ask a question here.



sir thank you for sharing this paper which will help students in their higher studies.
i am a fresh research student i hope this paper will be of great use to me taking interest in research in this area.
sir i am selecting this topic in my seminar presentation